CANA : CAlcul NAturel
Mots clés
Systèmes dynamiques discrets (non-)déterministes, probabilistes ou quantiques. Réseaux d’interaction : réseaux d’automates, automates cellulaires, piles de sable. Inspirations de et applications à la biologie et la physique
Responsable
Kevin PERROT
Membres
Post-doctorant
cameron.calk@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL, étage 4ème, bureau 04.31
Post-doctorant (ATER)
pablo.concha-vega@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL
Doctorant
nasra.daher-ahmed@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL, étage 5, bureau 05.22
Enseignant/Chercheur
giuseppe.dimolfetta@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL
Doctorant
niccolo.fonio@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL, étage 4, bureau 424
Doctorant
alienor.goubault-larrecq@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL
Doctorant
ugo.nzongani@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL, étage 4ème, bureau 04.06
Enseignant/Chercheur
kevin.perrot@lis-lab.fr
https://pageperso.lis-lab.fr/kevin.perrot/
Luminy, AMU TPR2 ET GRAND HALL, bureau 534
Enseignant/Chercheur
antonio.porreca@lis-lab.fr
https://aeporreca.org
Luminy, AMU TPR2 ET GRAND HALL, étage 5, bureau 532
Doctorant
marius.rolland@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL, étage 5ème, bureau 05.19
Enseignant/Chercheur
sylvain.sene@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL, bureau 534
Enseignant/Chercheur
pierre.siegel@lis-lab.fr
Luminy, AMU TPR2 ET GRAND HALL, bureau 513
Objectif scientifique
Le calcul naturel est un domaine de l’informatique fondé sur les liens que cette science entretient avec d’autres disciplines, en particulier la physique et la biologie. D’une part, il vise à abstraire des phénomènes naturels pour développer de nouveaux paradigmes de calcul et poursuivre l’analyse de modèles de calcul existants. D’autre part, il propose d’utiliser ces modèles pour mieux comprendre ces phénomènes et tâcher de dégager certaines des lois fondamentales qui semblent gouverner le monde qui est le notre.
L’équipe CANA (CAlcul NAturel) vise, en particulier, à mieux capturer les paradigmes de base de la biologie et de la physique théoriques, au travers d’approches issues de l’informatique fondamentale et des mathématiques discrètes. Ces approches et les méthodes qui leur sont associées, que nous développons également per se, reposent sur l’étude des interactions entre entités. Le plus souvent, les entités que nous étudions n’ont qu’un nombre fini d’états possibles, et interagissent localement sur le réseau où elles sont disposées, en pas de temps discret. Avec leur séduisante simplicité, ces modèles discrets permettent de capturer l’essence de la dynamique d’un grand nombre de systèmes naturels et donc d’en offrir une meilleure compréhension. À titre d’exemple, ces modèles permettent de représenter qualitativement, de par leur niveau d’abstraction élevé, des réseaux de régulation biologique, la propagation de particules en physique quantique ou encore l’émergence de vagues dans les tas de sable. Au delà de leur intérêt sur ces aspects de modélisation, ces modèles peuvent naturellement être étudiés et analysés en tant que tels, que ce soit pour leurs propriétés intrinsèques de dynamique, de complexité ou encore de calculabilité.
Définir des modèles discrets inspirés de phénomènes naturels, démontrer formellement leur pertinence, comprendre les comportements complexes qu’ils engendrent au moyen de résultats mathématiques rigoureux et s’en servir pour mieux comprendre les systèmes réels qui nous entourent : ces préoccupations sont celles qui animent les membres de l’équipe CANA, qui considèrent ainsi les modèles à la fois pour leur pouvoir représentationnel et pour leur capacité calculatoire.
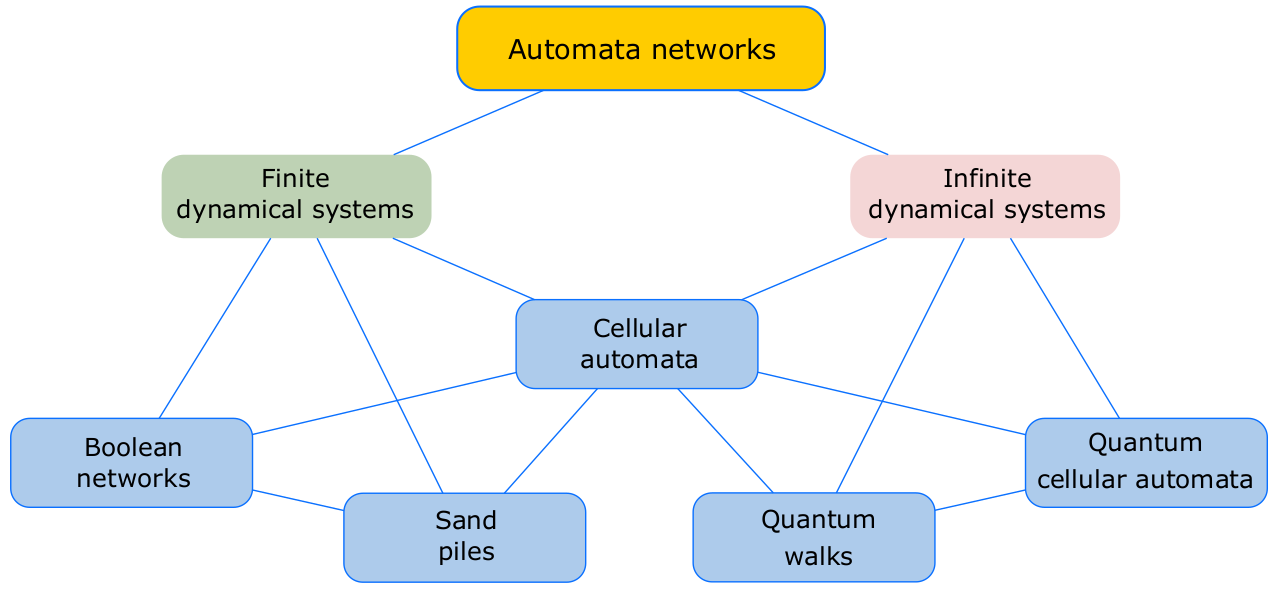
Selon les besoins des recherches menées, les modèles étudiés possèdent des particularités qui peuvent être d’ordre statique (syntaxique) ou dynamique (sémantique) : architecture des réseaux régulière ou non, déterminisme ou non des règles locales de transition des entités qui peuvent alors être probabilistes ou encore revêtir un caractère quantique, synchronisme ou asynchronisme de l’évolution des entités…
Quant aux méthodes qui se retrouvent au cœur des recherches menées par l’équipe CANA, elles sont majoritairement issues de la théorie des systèmes dynamiques discrets, de la combinatoire, de la théorie de la complexité et de la calculabilité, de la logique non-monotone et de l’information quantique.